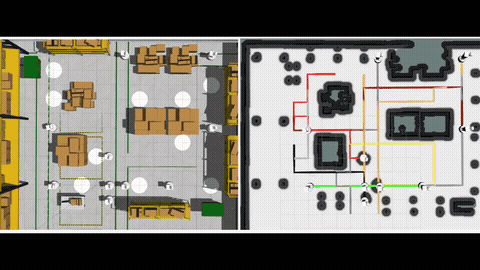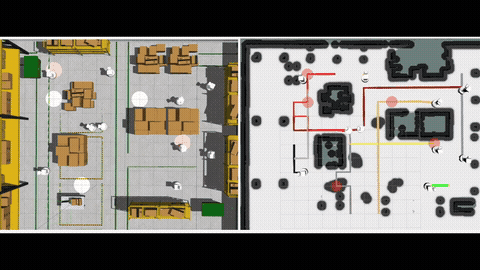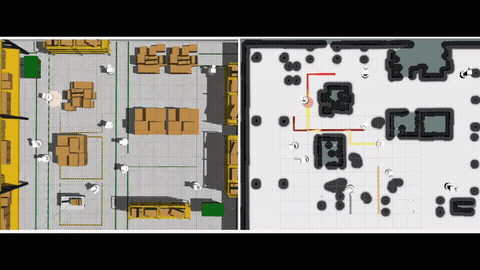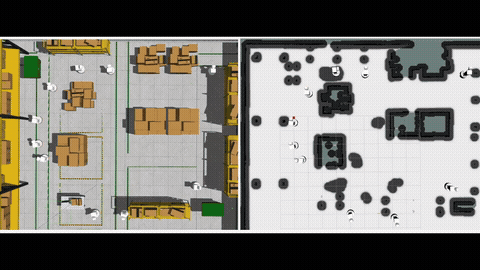
Robots have the potential to perform search for a variety of applications in different scenarios. In humanitarian assistance and disaster relief, it is often critical to find signs of life in the presence of conflicting criteria, objectives, and information. Ergodic search provides a framework for exploiting available information as well as exploring for new information, especially when time is of the essence. Ergodic search algorithms plan trajectories such that the time spent in a region is proportional to the amount of information in that region, and is able to naturally balance exploitation (myopically searching high-information areas) and exploration (visiting all locations in the search space for new information).
Multi-Objective Ergodic Search
Existing ergodic search algorithms, as well as other information-based approaches, typically consider search using only a single information map. However, in many scenarios, the use of multiple information maps that encode different types of relevant information is common. Ergodic search methods currently do not possess the ability for simultaneous nor do they have a way to balance which information gets priority. This leads us to formulate a Multi-Objective Ergodic Search (MOES) problem, which aims at finding a set of Pareto-optimal solutions, for the purpose of providing human decision makers various solutions that trade off between conflicting criteria.
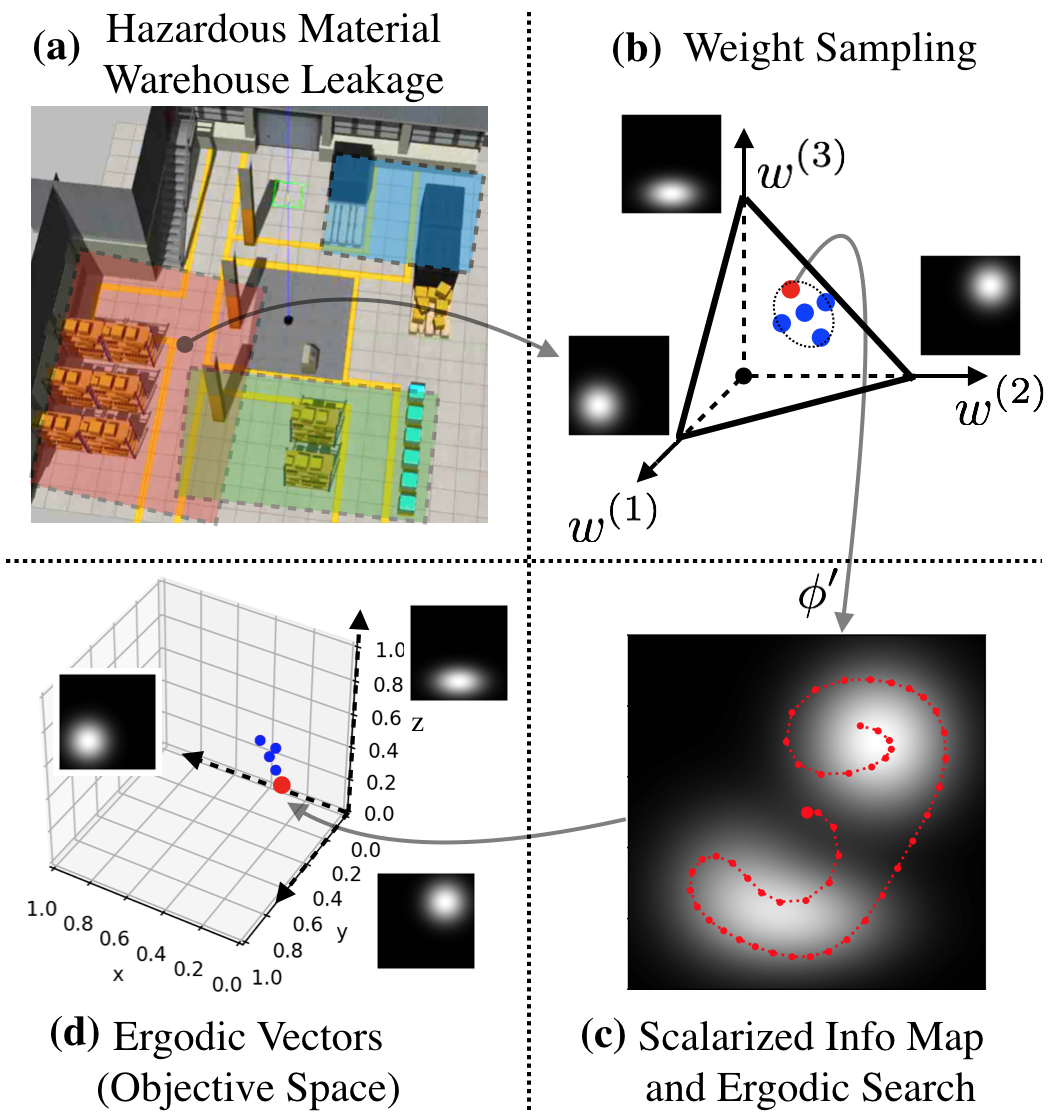
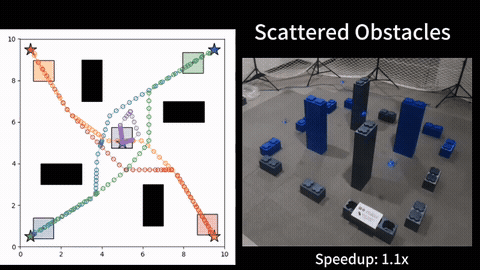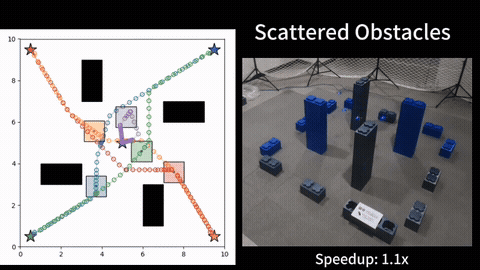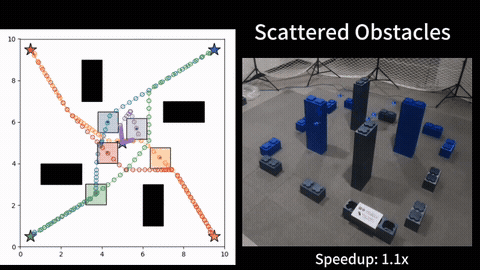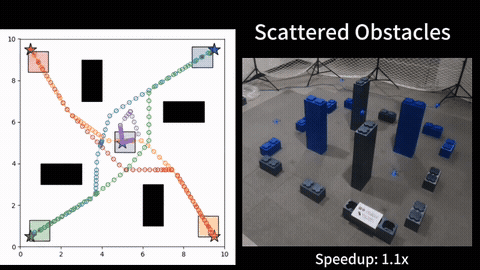
To efficiently solve MOES, we develop a framework called Sequential Local Ergodic Search (SLES) that converts a MOES problem into a “weight space coverage” problem. We formally prove that the trajectories computed by SLES is guaranteed to be Pareto-optimal. Furthermore, SLES leverages the idea of local optimization based on the inherent convexity of the ergodic metric in the Fourier coefficient space. To expedite the computation, we also develop a variant called Adaptive SLES, which can adjust the computation based on the similarity of the information maps in the Fourier coefficient space. Finally, we extend the method from single-agent to multi-agent and deploy it on two robots. Our numerical results show that SLES and A-SLES compute a set of solution trajectories with better ergodic metrics than applying Multi-Objective Genetic Algorithms to MOES. Additionally, our methods require less than half of the run time of a naive scalarization method that does not leverage local optimization. We simulate our method in a hazardous material warehouse in ROS/Gazebo, and verify that the planned trajectory can be executed on physical robots. More details can be find in [1].

Allocating Multiple Information Maps to Multiple Agents
A natural extension of MOES is to consider multiple robots. Instead of letting all robots to search all information maps, a natural question is how to assign the information maps to the agents, so that the robots collectively achieve better performance. We therefore formulate a multi-agent multi-objective ergodic search problem, with the primary focus on how to efficiently allocate the information maps to the agents. We seek to the optimize the worst-case scenario, i.e., the highest ergodic metric on any information map is minimized (minmax objective). The main challenge in determining the optimal allocation is the exponential growth of the number of possible allocations with the number of maps and agents. Further, computing the cost of an allocation is itself an expensive planning problem, since evaluating an allocation requires identifying the maximum ergodic metric with respect to the information maps, which requires computing the trajectory for each agent.
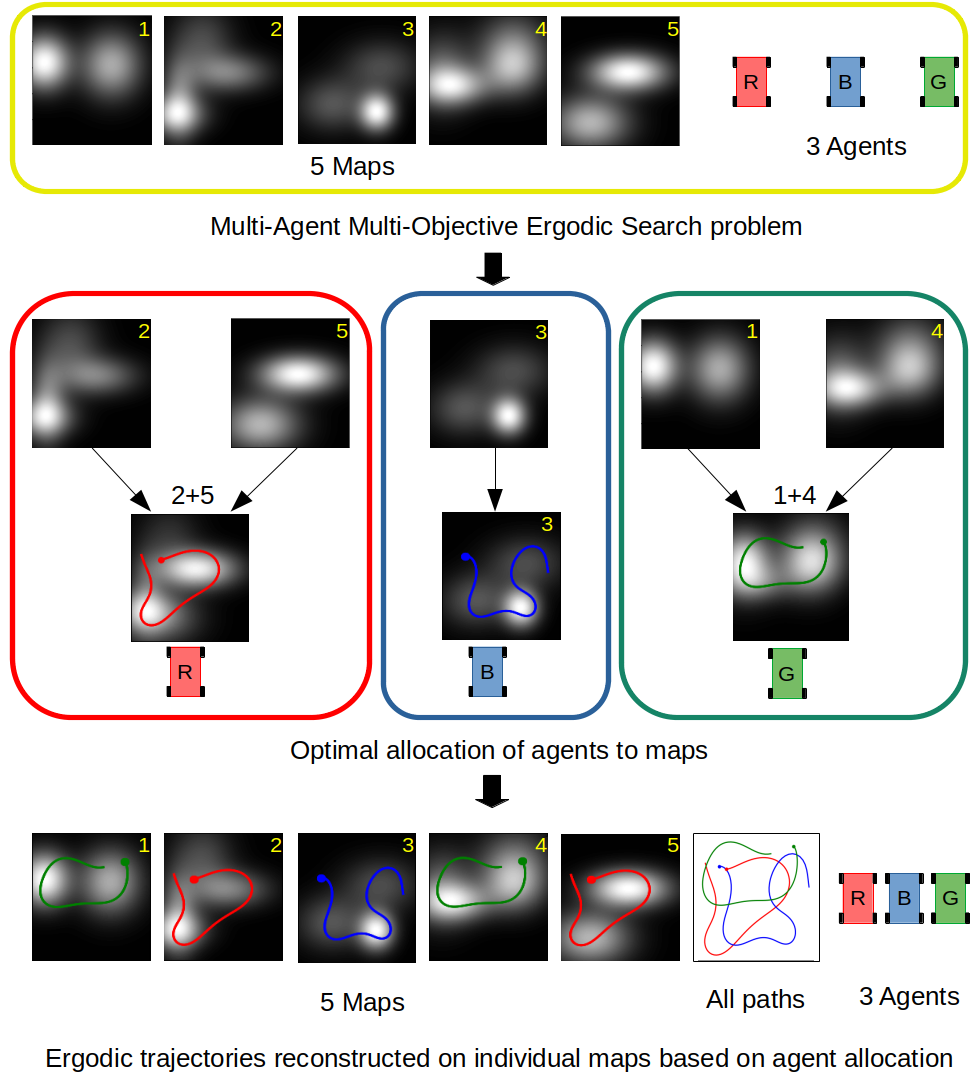
To mitigate the computational challenge, we present a branch and bound algorithm with pruning techniques that reduce the number of allocations to be searched to find the optimal allocation. To reduce the branching factor in branch and bound, we propose to cluster information maps before allocation based on the similarity among information maps. Clustering information maps decreases the number of possible allocations and thus the branching factor. Testing on 70 randomly generated test cases shows an order of magnitude improvement in runtime for our branch and bound approach compared to an exhaustive brute force approach. Using similarity clustering further reduces the runtime, while maintaining good solution quality with an average of 20\% deviation from the optimal minmax ergodic metric. More details can be found in [2].