This research is in collaboration with Anoop Bhat from Prof. Howie Choset’s group at CMU and Allen George Philip from Prof. Sivakumar Rathinam’s group at TAMU.
Traveling Salesman Problem (TSP) is one of the most well known NP-hard problem, which seeks a tour that visits each vertex (indicating a target location) in a graph exactly once while minimizing the travelled distance. This work investigates Moving Target TSP (MT-TSP), which generalizes TSP to the scenarios where the targets are moving and must be visited within given time windows. MT-TSP arises in applications where a robot arm inspects multiple moving items on a conveyer belt, or a drone needs to intercept multiple moving objects for surveillance. MT-TSP is difficult, as it not only inherits the combinatorial complexity of determining the visiting order of targets as TSP does, but also involves temporal constraints as the robot must reach the same location at the same time as each of the targets to visit.
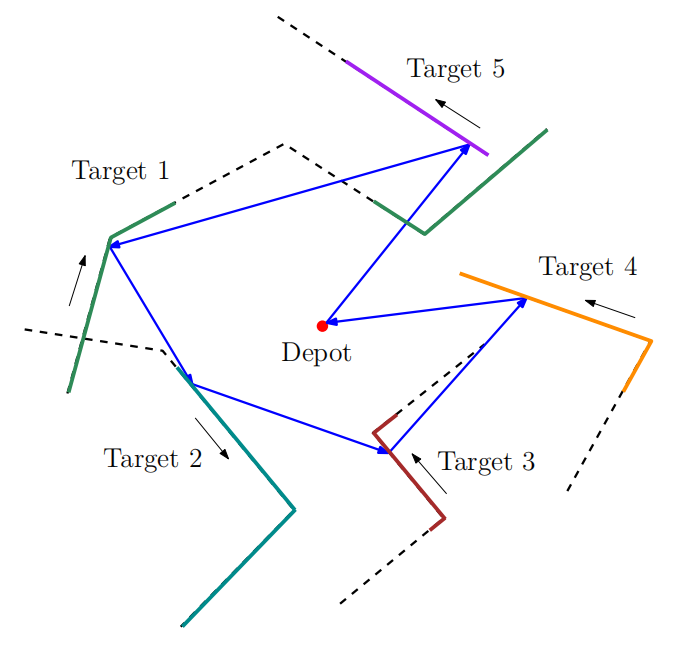
Our work begins with MT-TSP without considering any obstacles. We develop new bounding techniques to provide tight lower bound for the problem []. Our approach relies on relaxing the continuity constraints on the tour. This is done by partitioning the targets’ trajectories into small sub-segments and allowing the agent to arrive at any point in one of the sub-segments and depart from any point in the same sub-segment when visiting each target. This lets us pose the bounding problem as a Generalized Traveling Salesman Problem (GTSP) in a graph where the cost of traveling an edge requires us to solve a new problem called the Shortest Feasible Travel. We first prove that the proposed algorithms provide lower bounds to the MT-TSP. We also provide computational results to corroborate the performance for instances with up to 15 targets. For the special case where targets travel along lines, we compare our method with the existing SOCP based method. While the SOCP based method performs well for instances with 5 and 10 targets, ours outperforms the SOCP based method for instances with 15 targets. For the general case, on average, our approaches find feasible solutions within around 4% of the lower bounds for the tested instances.

We also develop a new mixed integer conic programming (MICP) formulation for MT-TSP that bypasses the big-M constraints of the existing formulation and thus able to provide tighter relaxation, which eventually leads to a faster exact approach for MT-TSP. The formulation relies on the key idea that when the targets move along lines, their trajectories become convex sets within the space-time coordinate system, which allows us introducing new decision variables, representing the problem using graph of convex sets, and convexifying the corresponding constraints. The experimental results show that our formulation outperforms the existing formulation for instances with up to 20 targets, with up to two orders of magnitude reduction in runtime, and up to a 60\% tighter optimality gap. We also show that the solution cost from the convex relaxation of our formulation provides significantly tighter lower bounds for the MT-TSP than the existing ones. More details can be found in [1].
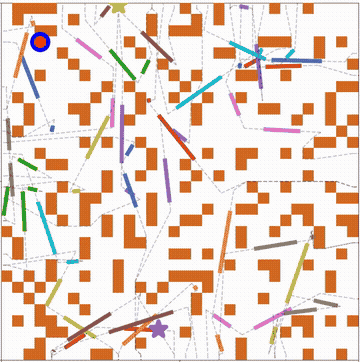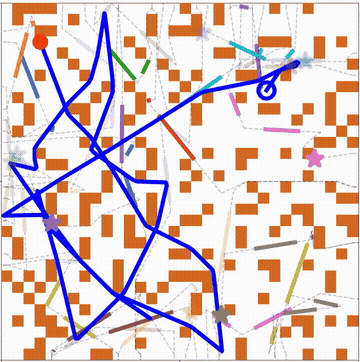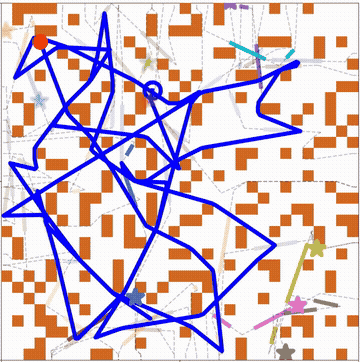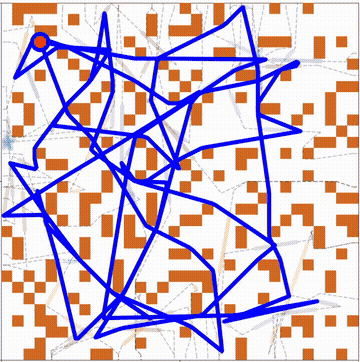
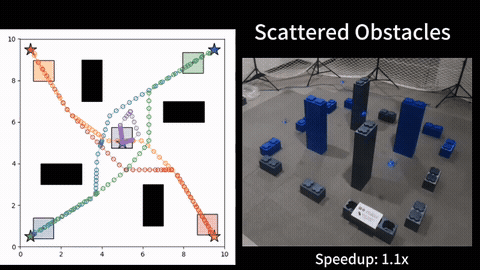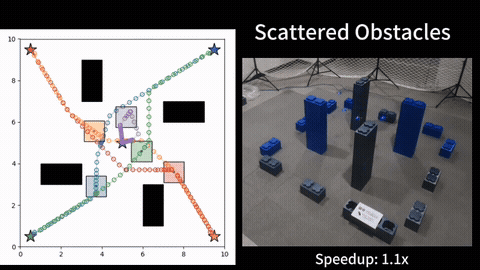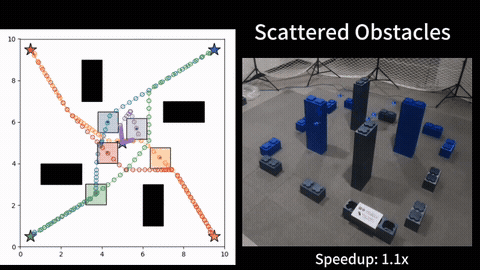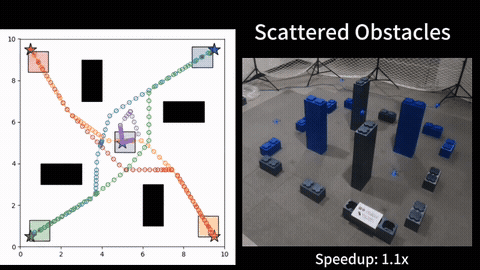
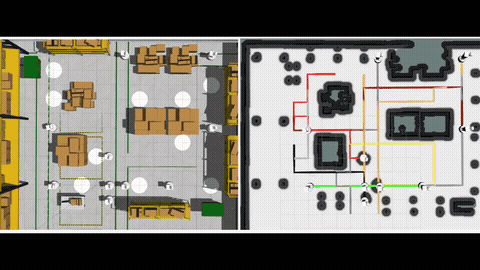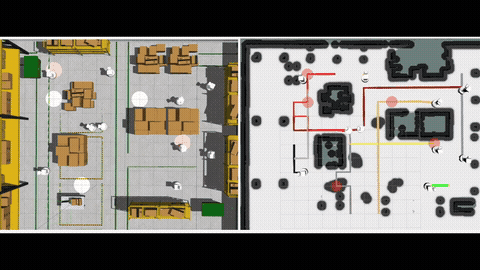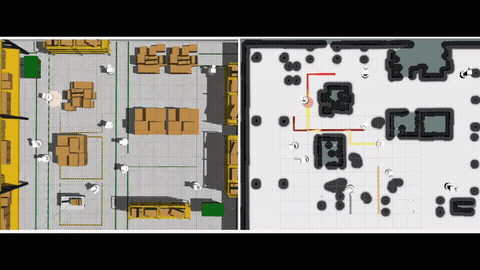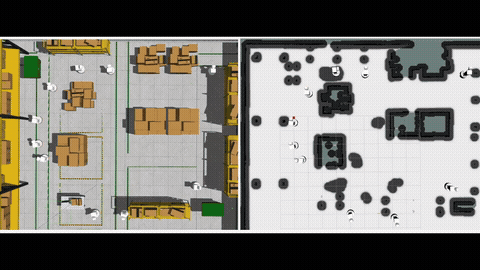
We further consider obstacles in the workspace and address the moving target traveling salesman problem with obstacles (MT-TSP-O). We develop a complete algorithm for finding feasible solutions to the MT-TSP-O. Our algorithm builds a tree to systematically find target sequences, and runs a sequence of A* searches, each on a new visibility graph for moving targets, to find trajectories intercepting the targets. Our approach finds feasible solutions in all cases where the baseline does, and sometimes finds a feasible solution with up to 38 times less computation time. More details can be found in [2].