Connectivity maintenance is of fundamental importance for multi-robot systems in applications such as search and rescue, robust navigation in harsh environments, etc. In general, connectivity maintenance contradicts with other planning objectives (say the main task) such as minimizing arrival time or maximize information collection efficiency, in a sense that maintaining connectivity often forces the robots to deviate from their optimal task trajectories so that they can build inter-robot connections.
Existing Connectivity Maintenance Strategies
Various strategies have been proposed to maintain connectivity, ranging from continual connectivity that requires all robots to stay connected at all times, periodic connectivity that requires all robots to regain connectivity at pre-defined fixed intervals, to intermittent connectivity that allows the robots to meet at some locations intermittently over time without enforcing a fixed time interval between two subsequent connections.
Most existing approaches seek to explicitly determine the connection location and time (or schedule), either in a joint optimization or in a sequential fashion. This project takes the view that, although such explicit determination can guarantee connection frequency and quality, but may restrict the robots motion “too much” and thus lower the efficiency for the main task. This project therefore explores a new idea of maintaining intermittent connectivity in a soft manner based on the distribution of robots’ trajectories.
Our New Probabilistic Measure
We introduce a novel probabilistic measure for characterizing inter-robot connectivity based on the time-averaged statistics of robot trajectories. The proposed measure attempts to avoid explicitly formulating the connection locations, times, and topologies as the planning objective or constraints, or imposing any hard constraints on connectivity. Instead, we seek to infer the probability of connection among the robots based on the distribution of their trajectories as the time horizon goes to infinity. Such a measure provides a new way to impose intermittent connectivity constraints as soft constraints for trajectory optimization, and allows us to formulate a corresponding optimal control problem (OCP) that considers both main trajectory optimization problem and connectivity maintenance.
Instantiation with Ergodic Search
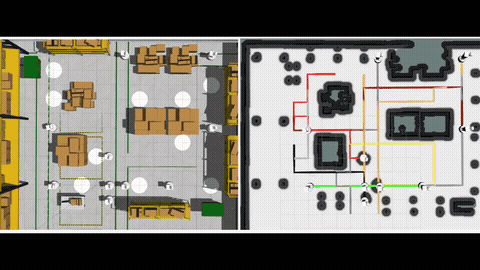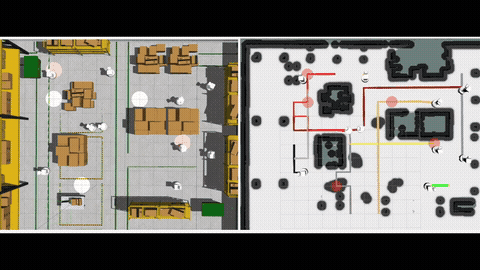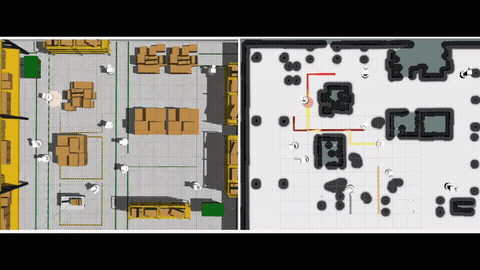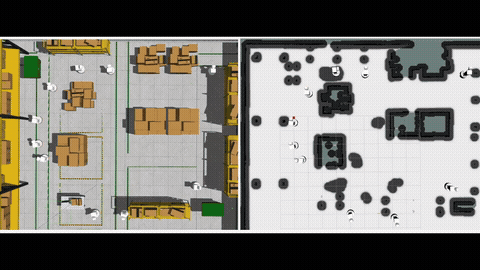
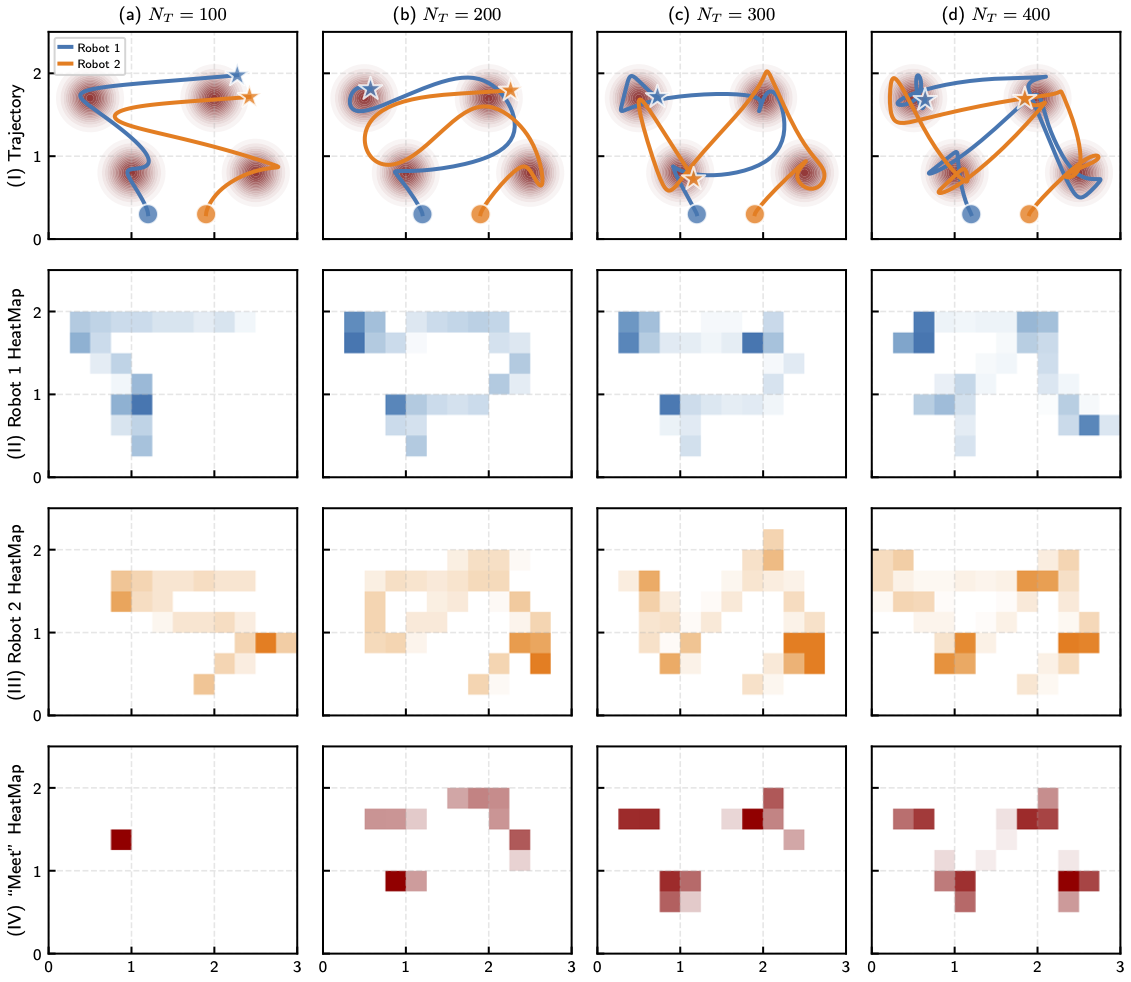
We instantiate this idea together with ergodic search, a method for information gathering that can inherently balance between exploration (visit all locations for information) and exploitation (greedily search high information regions), by planning trajectories such that the amount of time the robots spend in a region is proportional to the amount of information in that region. (See more on ergodic search)[] We formulate an optimal control problem called Multi-agent Ergodic search with Connectivity maintenance (MEC) that considers both ergodic trajectory optimization and connectivity maintenance. To solve the MEC problem, in theory, we show how to rewrite this optimal control problem into a standard Bolza form, and derive the condition for optimality based on the Pontryagin principle. In practice, we provide an algorithm called IMEC (I=iterative) based on the augmented Lagrangian method (ALM) and iterative linear quadratic regulator (iLQR) that can numerically solve the MEC problem.
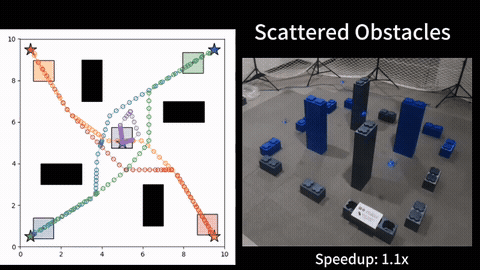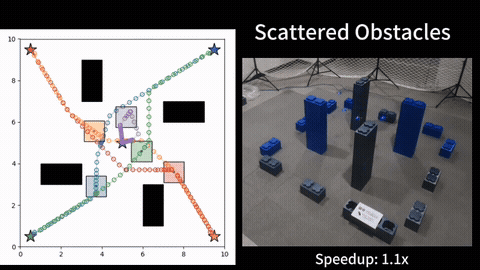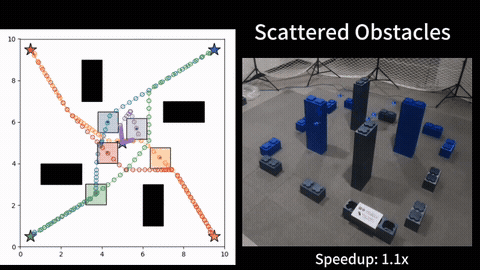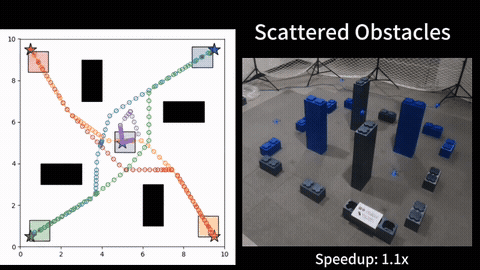
Our experimental results verify the effectiveness of the proposed probabilistic measure, as we observe a positive correlation between the value of the measure and the actual connection time between the robots along their planned trajectories. Additionally, the results show that the ergodic search combined with our measure achieves better ergodic metrics than the baseline approaches, and the robots can intelligently balance between ergodic search and connectivity maintenance in the long run. Finally, we showcase the use of our planner on a multi-drone system in our lab at SJTU. More details can be found in our paper [1].
