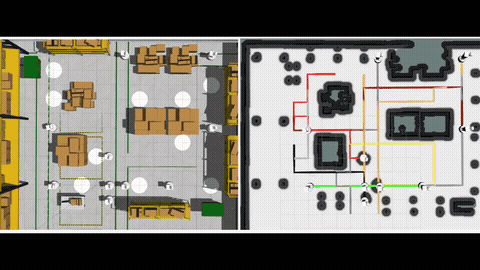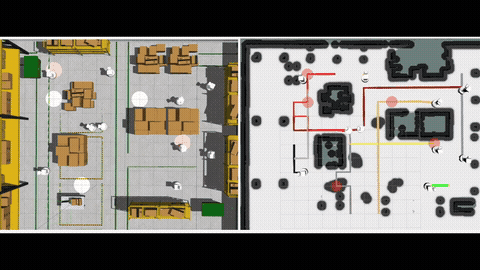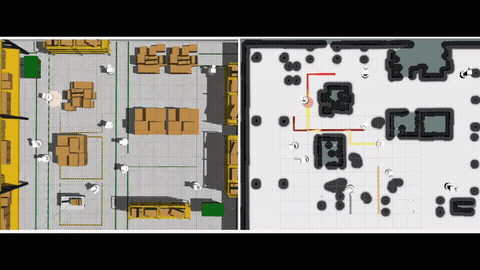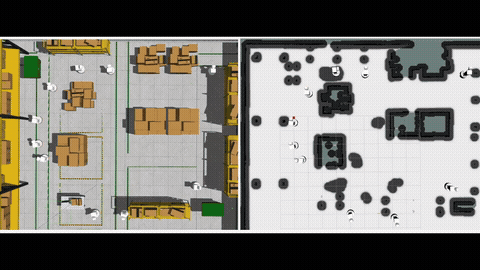
Multi-Agent Path Finding (MAPF) computes a set of collision-free paths for multiple agents connecting their respective start and goal locations while optimizing a scalar measure of paths. We investigate a natural generalization of the MAPF to include multiple objectives for multiple agents and hence the name Multi-Objective Multi-Agent Path Finding (MOMAPF). In MOMAPF, agents have to trade-off multiple objectives such as completion time, travel risk and other domain-specific measures. MOMAPF is a generalization of MAPF and is therefore NP-Hard to solve to optimality.
In the presence of multiple conflicting objectives, in general, no (single) solution can simultaneously optimize all the objectives. Therefore, the goal of MOMAPF is to find the set of all Pareto-optimal solutions rather than a single optimal solution as in MAPF. A solution is Pareto-optimal if there exists no other solution that will improve one objective without deteriorate at least one of the other objectives. To solve MOMAPF, we leverage both the dominance principles in multi-objective optimization and multi-agent path planners to develop new algorithms.
Multi-Objective M* (MOM*)
MOM* begins by ignoring agent-agent collision and solve a single-agent multi-objective path planning problem to find individual Pareto-optimal paths. These individual paths can be readily converted to an individual policy that maps the location of the agent to an action in order to direct the agent from its starting location to its goal. MOM* lets the agents follow their individual policies towards their goals, unless a collision is detected. When a collision is found, MOM* couples the agents together, which locally increases the dimensionality of the search space and MOM* plans a path in the joint configuration space of these agents to resolve the collision. During this search process, to compare two paths in the presense of multiple objectives, MOM* leverages the dominance rules. As a result, MOM* plans in a compact space to find all Pareto-optimal solutions, and requires less computational effort than directly searching in the joint configuration space of agents. Additionally, with inflated heuristics, MOM* can be modified to a bounded sub-optimal algorithm that trades off between computational efficiency and approximation quality.
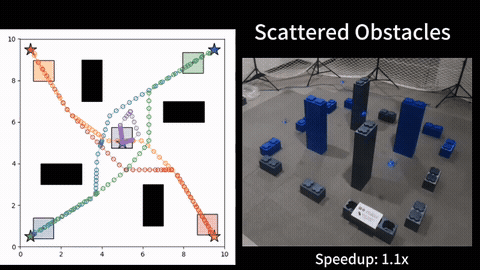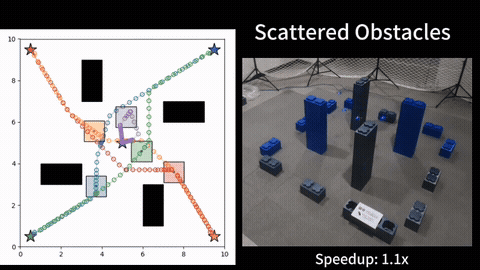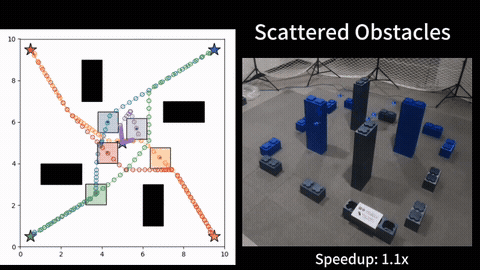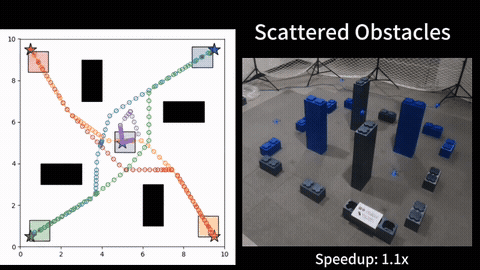
To evaluate MOM*, we ran tests in various grid-like maps, against using multi-objective A* like search in the joint configuration space of the agents. We compared the algorithms under multiple metrics, as functions of both the number of agents as well as the number of objectives. The results show that MOM* runs faster than the baseline, and the heuristic inflation further speeds up the MOM* at the cost of finding a bounded sub-optimal Pareto-optimal solution set. More details can be found in [1].
Multi-Objective Conflict-Based Search (MO-CBS)
Among the algorithms that optimally solve the single-objective MAPF problems, Conflict-Based Search (CBS) has received significant attention due to its computational efficiency on average. We therefore investigate how to extend CBS to handle multiple objectives, which leads to a new algorithm called Multi-Objective Conflict-Based Search (MO-CBS).
Similar to CBS, MO-CBS is a two-level search algorithm. The high-level search detects and resolves agent-agent collision by adding constraints to the agents while the low-level search plans paths for a single agent while satisfying the added constraints. MO-CBS begins by finding a Pareto-optimal set of (individual) paths for each single agent ignoring any agent-agent collision and then takes all combinations of these paths over all the agents to form a set of joint paths, where a joint path is a set of paths with one path for each agent. MO-CBS then creates a constraint tree for each joint path for the high-level search. In a joint path, if two agents occupy the same location at the same time, a conflict happens. To resolve a conflict between two agents, a constraint is added to either of the agents, and the low-level search finds a new Pareto-optimal set of paths for that agent while satisfying all constraints. Each of these paths results in a new branch for future search. MO-CBS uses dominance rules to select candidate solutions for conflict checking and compares them until all the candidates are either pruned or identified as Pareto-optimal. More details can be found in [2].
TODO… more…