For many motion planning problems, there is currently no algorithm available in the literature to find an optimal solution. While finding the optimum is challenging, there are many algorithms that can compute a feasible solution such as search-based or sampling-based methods. A natural and fundamental question is: how close a feasible solution actually is to the (true) optimum. In the absence of methods for finding the optimum, lower bounds can be used as proxies to the optimum. Baseline approaches that find trivial lower bounds are always possible. However, these bounds tend to be far away from the optimum, and therefore, do not serve as good estimates of the optimum. The goal of this research is to develop approaches that can provide tight lower-bounding estimates of the true optimum to motion planning problems.
Optimality Bounds for the Motion Planning Among Dynamic Obstacles
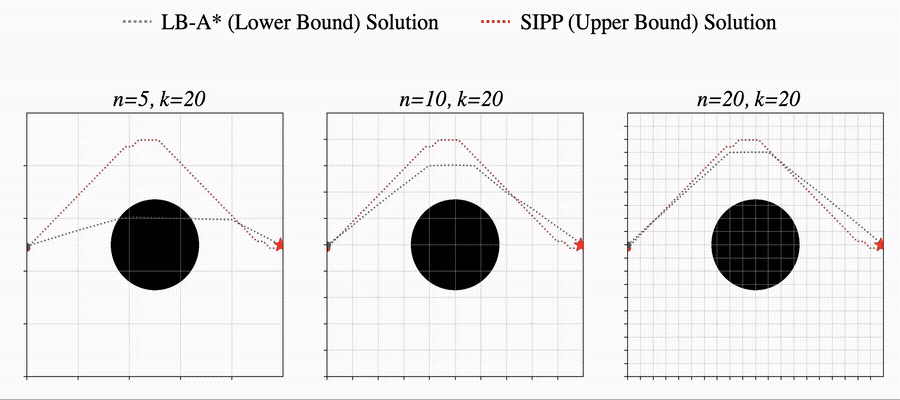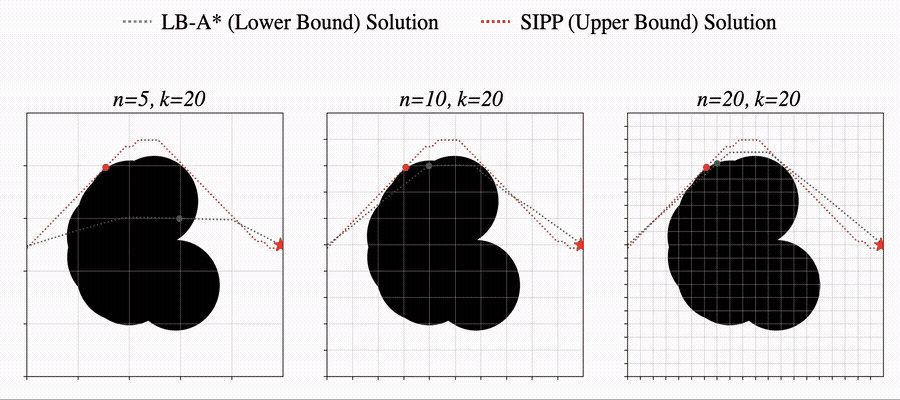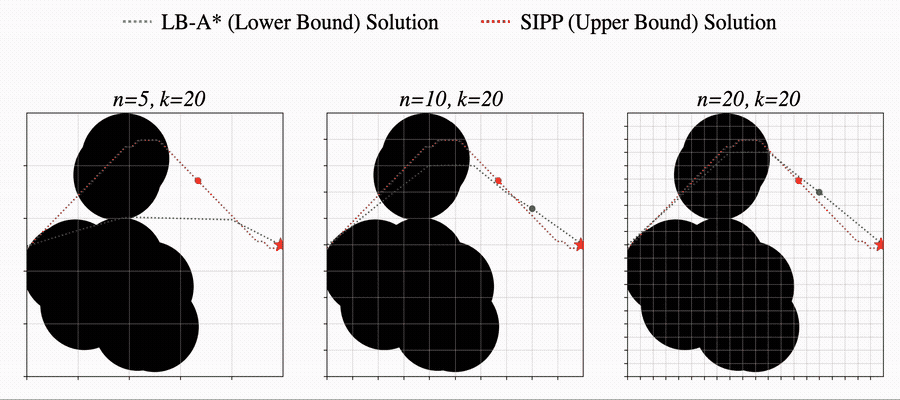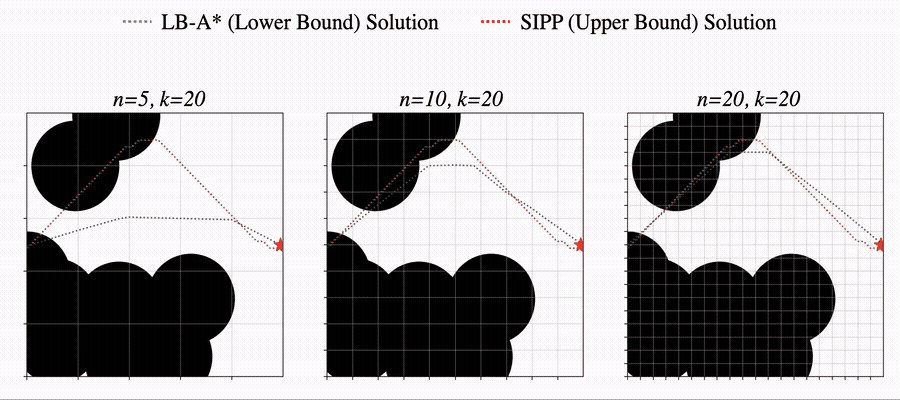
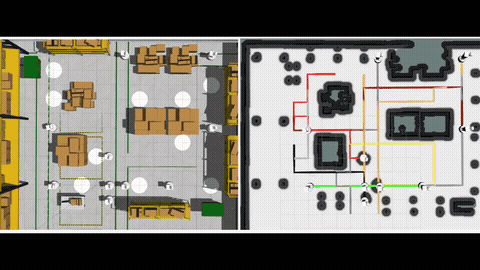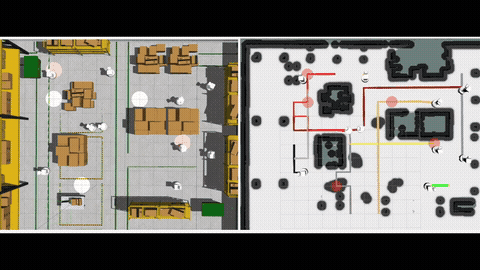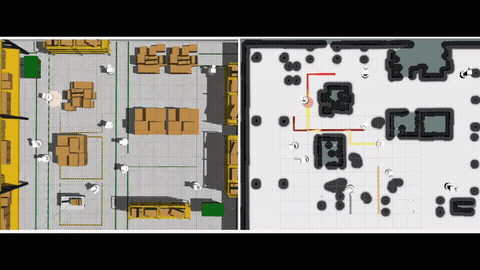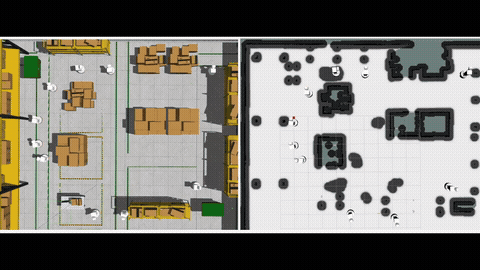
We begin by considering a Motion Planning Problem with Dynamic Obstacles (MPDO) in 2D that requires finding a minimum-arrival-time collision-free trajectory for a point robot between its start and goal locations amid dynamic obstacles moving along known trajectories. We develop an approach that can provide tight lower bounds to the optimum, which consists of (i) a bi-level discretization approach that converts the MPDO to a relaxed path planning problem, and (ii) an algorithm that can solve the relaxed problem to obtain lower bounds. The proposed bi-level discretization approach simultaneously handles the collision avoidance constraints and the generation of tight lower bounds. We theoretically show that our approach generates lower bounds and the experimental results show that the bounds obtained by our approach for some instances are up to twice tighter than a baseline approach showcasing potential advantages of the proposed approach. More details can be found in [1].
Optimality Bounds for the Moving Target Traveling Salesman Problem
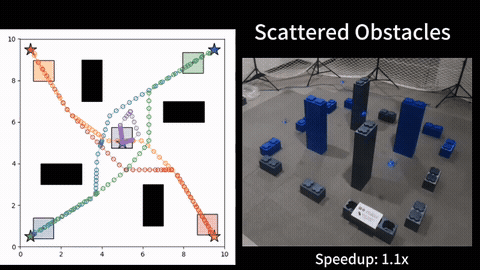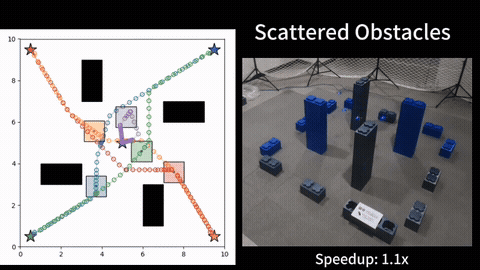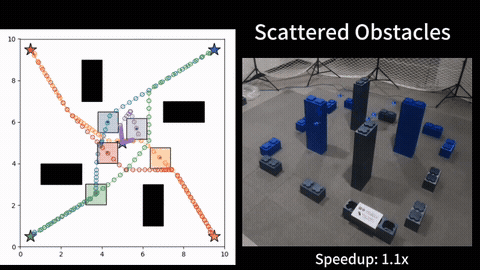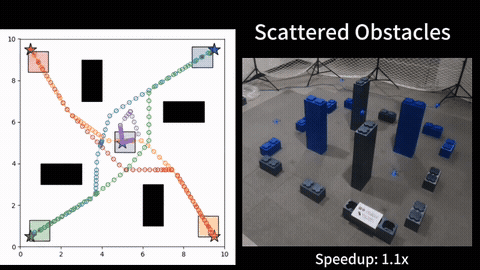
In collaboration with Prof. Rathinam, we then investigate Moving-Target Traveling Salesman Problem (MT-TSP). Given a set of target locations (or targets) and the cost of traveling between any pair of targets, the well-known TSP aims to find a shortest tour for a vehicle to visit each of the targets exactly once. Here, we consider a natural generalization of the TSP where the targets are mobile and traverse along known trajectories. The targets also have time-windows during which they must be visited. This generalization is motivated by applications in border surveillance, search and rescue, and dynamic target tracking where vehicles are required to visit or monitor a set of mobile targets. We refer to this generalization as the Moving-Target Traveling Salesman Problem, or MT-TSP for short. The focus of this work is on the optimality guarantees for the MT-TSP.
We introduce a new bounding approach called Continuity* (C*) that provides optimality guarantees to the MT-TSP. Our approach relies on relaxing the continuity constraints on the agent’s tour. This is done by partitioning the targets’ trajectories into small sub-segments and allowing the agent to arrive at any point in one of the sub-segments and depart from any point in the same sub-segment when visiting each target. This lets us pose the bounding problem as a Generalized Traveling Salesman Problem (GTSP) in a graph where the cost of traveling an edge requires us to solve a new problem called the Shortest Feasible Travel (SFT). We also introduce C*-lite, which follows the same approach as C*, but uses simple and easy to compute lower-bounds to the SFT. We first prove that the proposed algorithms provide lower bounds to the MT-TSP. We also provide computational results to corroborate the performance of C* and C*-lite for instances with up to 15 targets. For the special case where targets travel along lines, we compare our C* variants with the second-order conic programming (SOCP) based method, which is the current state-of-the-art solver for MT-TSP. While the SOCP based method performs well for instances with 5 and 10 targets, C* outperforms the SOCP based method for instances with 15 targets. For the general case, on average, our approaches find feasible solutions within around 4 percent of the lower bounds for the tested instances.