Multi-Agent Path Finding (MAPF) computes a set of collision-free paths for multiple agents from their respective starting locations to destinations. This work considers a generalization of MA-PF called Multi-Agent Teamwise Cooperative Path Finding (TCPF), where agents are grouped as multiple teams and each team has its own objective to be minimized. This work considers a generalization of MAPF, called Multi-Agent Teamwise Cooperative Path Finding (TCPF), where agents are grouped into multiple teams, and each team optimizes its own objective. Specifically, each agent has its own start and goal and belongs to at least one team. Every team has its own objective such as min-sum or min-max. As there are more than one teams in general, TCPF optimizes an objective vector, where each element of the vector corresponds to the objective of a team. For vector optimization, in general, there is no single solution that simultaneously optimizes all objectives. The problem thus seeks a set of Pareto-optimal solutions.
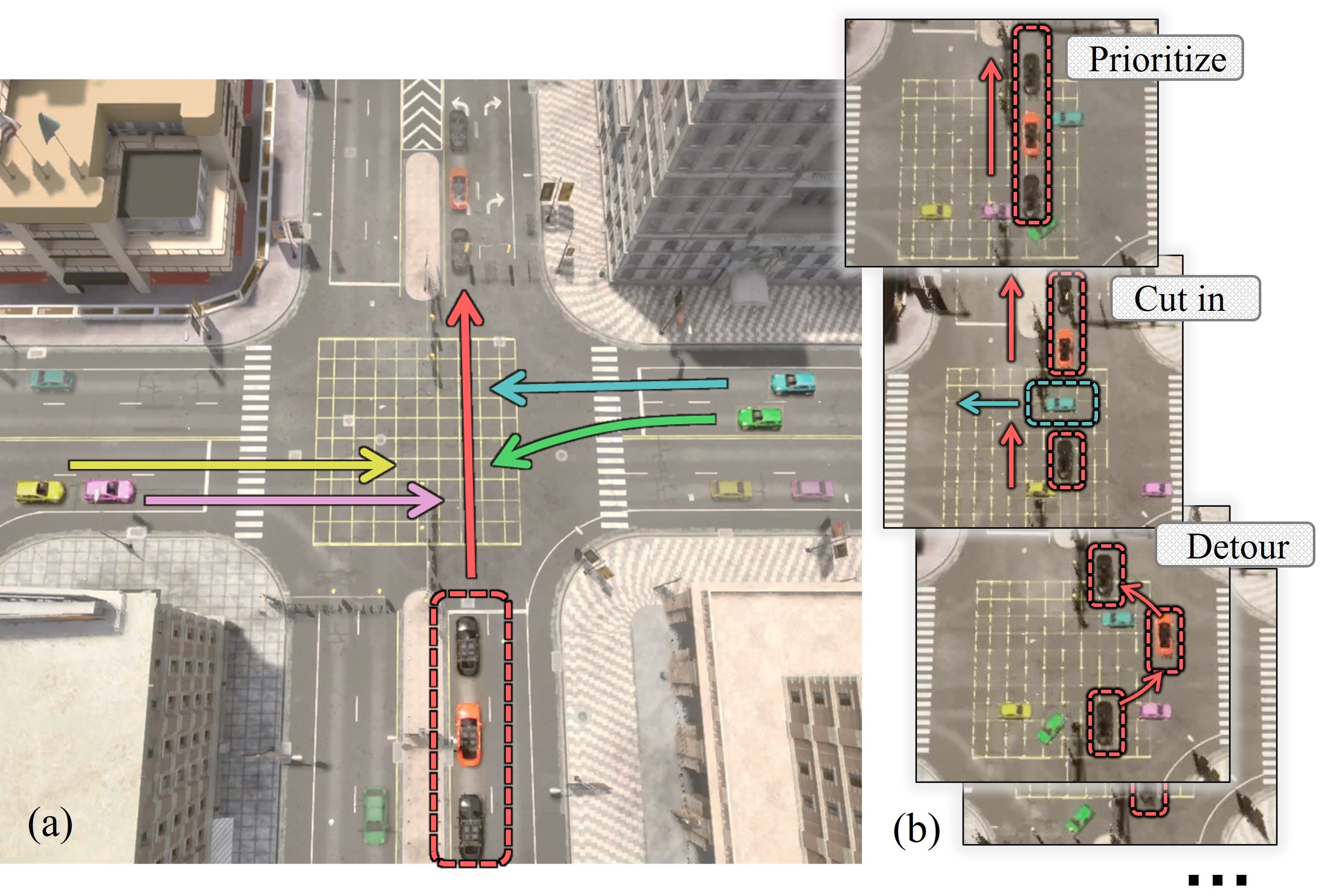
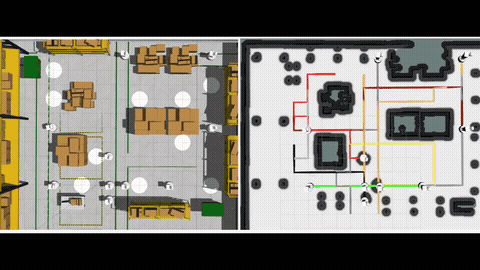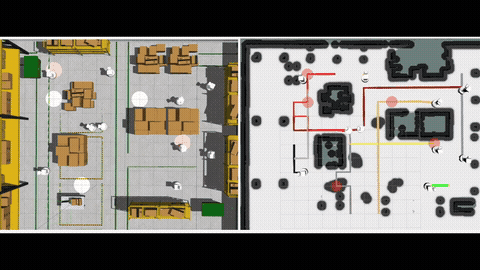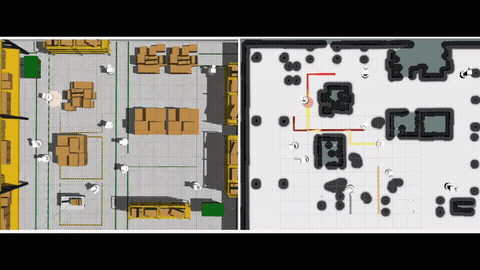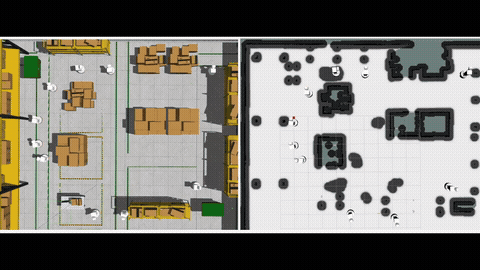
A motivating example of TCPF can be found in intersection coordination of connected autonomous vehicles. See Fig. 1 for an example, where a motorcade goes through an intersection that is shared with vehicles from other directions. The motorcade and all other vehicles naturally form two teams, and each team seeks to minimize their own traversal time through the intersection. The motion coordination has to trade the traversal time of one team for the other, and the set of Pareto-optimal solutions unveils trade-offs between the teams (Fig. 2), which can potentially support the intelligent decision making in traffic management.
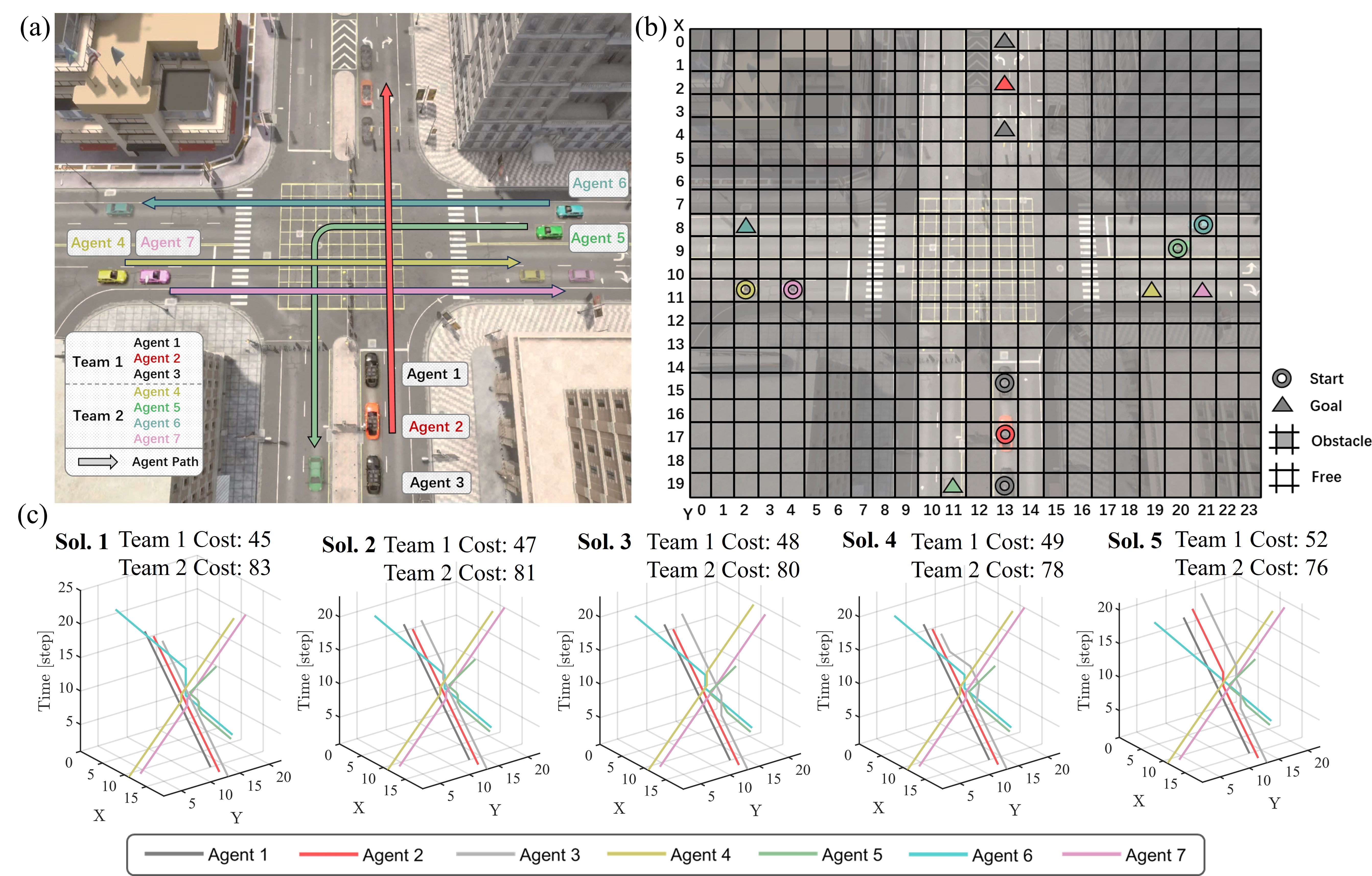
We formulated the TCPF problem, developed planners based on M* and CBS to solve it, and analyzed the properties of these planners [1]. For the experiments, we connect TCPF with traffic management in scenarios where all vehicles are fully autonomous, conencted and can be coordinated in a centralized fashion [2]. We also consider a special case of TCPF, a bi-objective MAPF problem that seeks to simultaneously minimize both the min-sum and the min-max objective of all agents. Here, min-sum and min-max are two widely used objective functions in MAPF, each with its own set of specialized algorithms. Our approach can solve it to optimize both objectives simultaneously.
