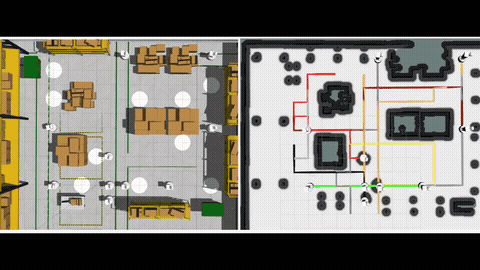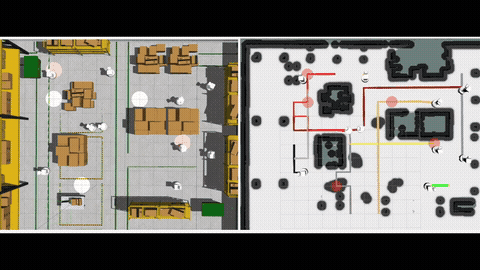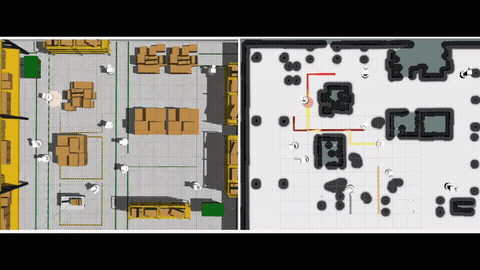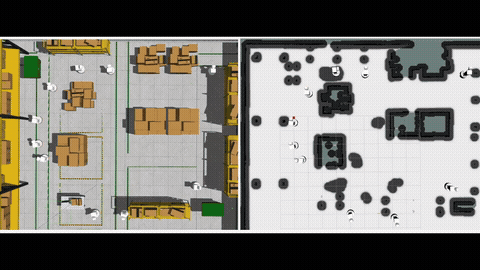
Multi-Agent Motion Planning (MAMP) is a fundamental problem in multi-robot systems, which seeks collision-free trajectories for multiple robots from their respective start to goal locations among static obstacles while reaching their goals as quick as possible. MAMP arises in applications such as logistics and surveillance. Consider autonomous guided vehicles or forklifts transporting materials in factories, or drones flying in a city to delivery packages in a coordinated fashion among buildings. MAMP naturally arises in these scenarios to optimize the operation of the robots. MAMP is challenging when producing high quality trajectories among obstacles while avoiding agent-agent collision. Existing approaches for MAMP include graph-based, Mix-Integer Programming (MIP) based and trajectory optimization-based, each with its own limitations. We propose approaches for MAMP based on Mixed Integer Conic Programming (MICP) and Graphs of Convex Sets (GCS) that complements these existing approaches.
CB-GCS: Conflict-Based search on the Graph of Convex Sets
To begin with, we leverage the recent notion of Graphs of Convex Sets (GCS), a new formulation for motion planning using conic programming, and investigates how to handle MAMP using GCS. In particular, we need to properly address the inter-robot collision avoidance constraints. We propose Conflict-Based search on the Graph of Convex Sets (CB-GCS), a new approach for MAMP. On one hand, CB-GCS leverages Conflict-Based Search (CBS) for Multi-Agent Path Finding (MAPF) problems, a technique that resolves agent-agent collisions in a discretized graph representation of the workspace. CB-GCS adapts the conflict resolution techniques from CBS to continuous space to resolve agent-agent collisions. On the other hand, CB-GCS leverages the recent concept of the Graph of Convex Sets (GCS), which has been used to plan paths in continuous spaces for a single robot navigating among static obstacles. CB-GCS plans a path for each agent in a time-augmented GCS, which includes an additional time dimension, to avoid agent-agent conflicts. Additionally, CB-GCS leverages anytime focal search to resolve agent-agent conflicts more efficiently while achieving a bounded suboptimal solution for MAMP. The results show that CB-GCS can find cheaper (better) solutions (i.e., up to 10x smaller optimality gap) than the baseline at the cost of limited scalability. More detail can be found in [1].
MICP: Mixed Integer Conic Programming
We then investigate directly using Mixed Integer Conic Programming (MICP) for MAMP, which bypasses the time-augmented GCS in CB-GCS and turns out to run faster in our experiments. Our method leverages the big-M techniques to formulate inter-robot collision avoidance constraints, and formulates the speed limits and Euclidean travel distance using conic constraints. We compare MICP with a recent sampling-based method, as well as different formulations. The experiments include several non-trivial settings with up to 10 agents. The results show that our approach can find high-quality solutions in challenging cluttered space. In other settings, the solutions found by our approach are around 8 times closer to the true optimum than the ones found by the sampling method when given the same amount of runtime. We also showcase the use of our approach on multiple drones under a motion capture system in non-trivial cluttered environments. More detail can be found in [2].
