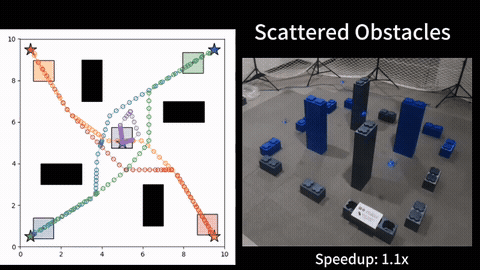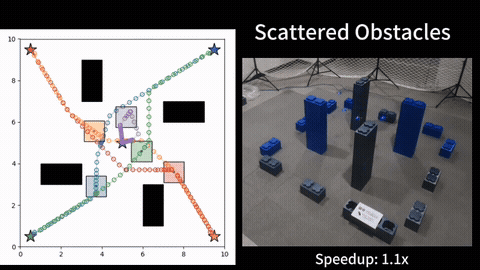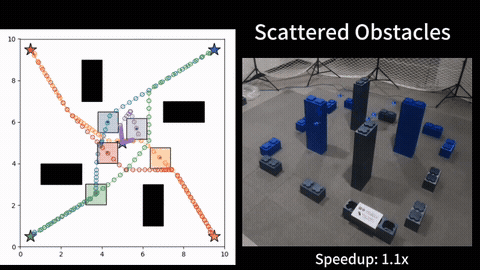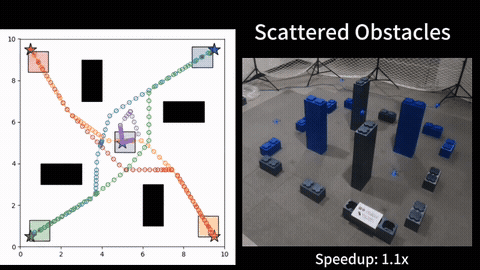
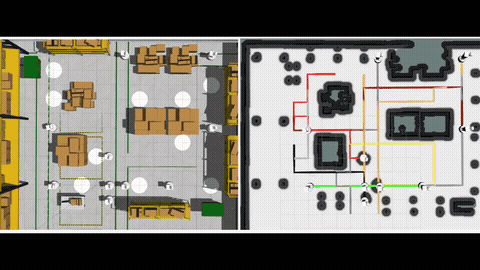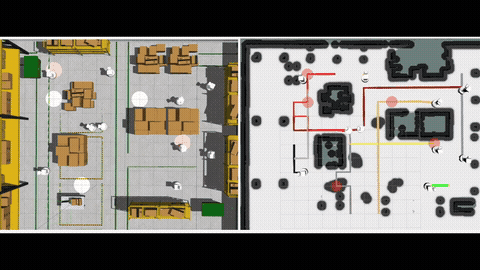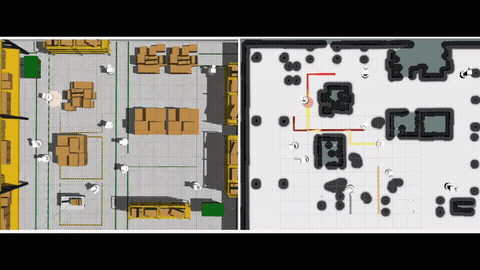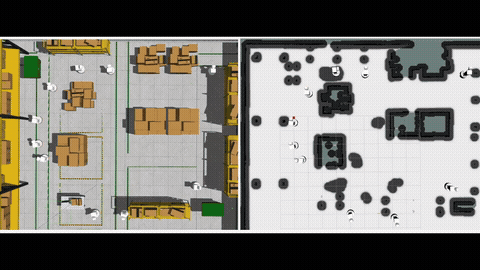
Given a graph with non-negative scalar edge costs, the well-known shortest path problem (SPP) requires computing a minimum-cost path from the given start node to a destination node in the graph, which be solved by Dijkstra or A*. We consider an extension of SPP, the Multi-Objective Path Planning (MOPP) problem, which generalizes SPP by associating each edge with a non-negative cost vector (of constant length), where each component of the vector corresponds to an objective to be minimized. MOPP arises in many applications including hazardous material transportation, robot design, and logistics, and is also the foundation for many other problems such as constrained path planning and route planning.
EMOA*: Fast Search for MOPP
In the presence of multiple conflicting objectives, in general, no (single) feasible path can simultaneously optimize all the objectives. Therefore, the goal of MOPP is to find a Pareto-optimal set (of solution paths), whose cost vectors form the so-called Pareto-optimal front. A path is Pareto-optimal (also called non-dominated) if no objective of the path can be improved without deteriorating at least one of the other objectives.
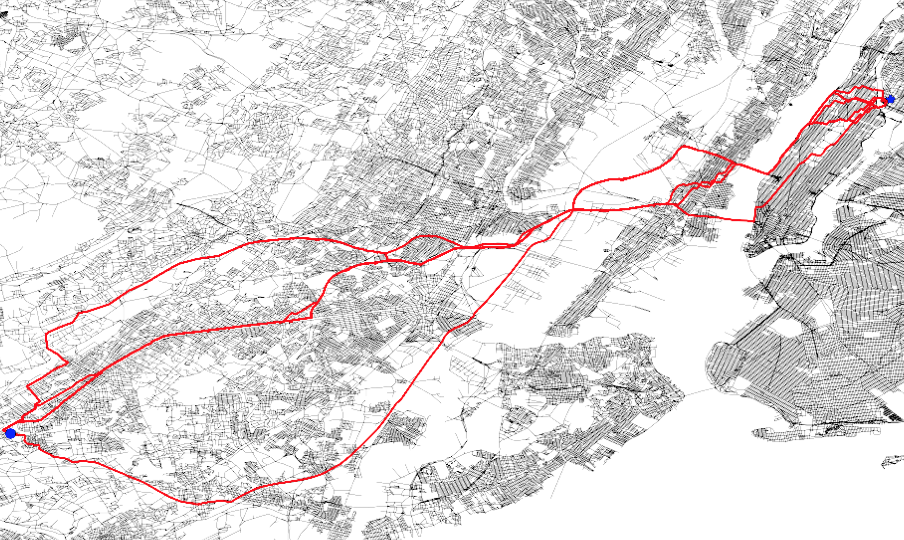
To solve MOPP, a family of approaches based on MOA* have been developed. Typically, these approaches maintain a “frontier” set at each vertex during the search process to keep track of the non-dominated, partial paths to reach that vertex. This search process becomes computationally expensive when the number of objectives increases as the number of Pareto-optimal solutions becomes large. We introduce a new method to efficiently maintain these frontiers for multiple objectives by incrementally constructing balanced binary search trees within the MOA* search framework. We show that our approach correctly finds the Pareto-optimal front, and then provide extensive simulation results for problems with three, four and five objectives to show that our method runs faster than existing techniques by up to an order of magnitude. [1][2].
MOPBD*: Incremental Search for MOPP in Dynamic Environments
We further consider MOPP in graphs with changing edge costs that represents dynamic environments. This problem arises robot navigation, where the robot needs to frequently update its graph representation of the workspace by incorporating new sensor reading such as unexpected closed doors, untraversable rough terrains, etc. In these scenarios, the robot needs to quickly replan its paths after the grpah changes. To achieve this goal, the existing incremental search algorithms, such as D* Lite, reuse previous, and perhaps partial, searches to expedite subsequent path planning tasks. We are interested in developing incremental search algorithms for path finding problems to simultaneously optimize multiple objectives such as travel risk, arrival time, etc. This is challenging because in a multi-objective setting, the number of Pareto-optimal solutions can grow exponentially with respect to the size of the graph.
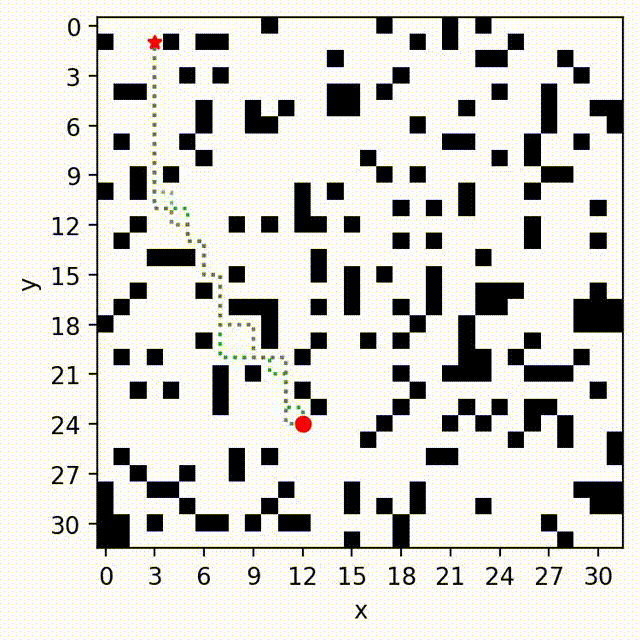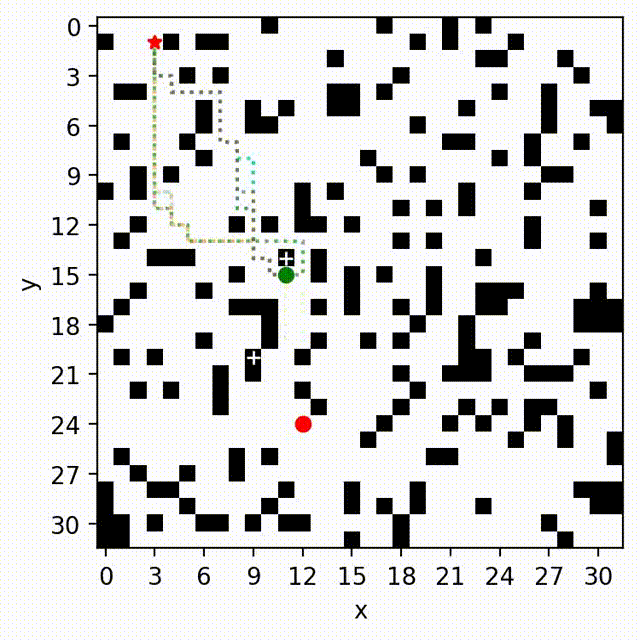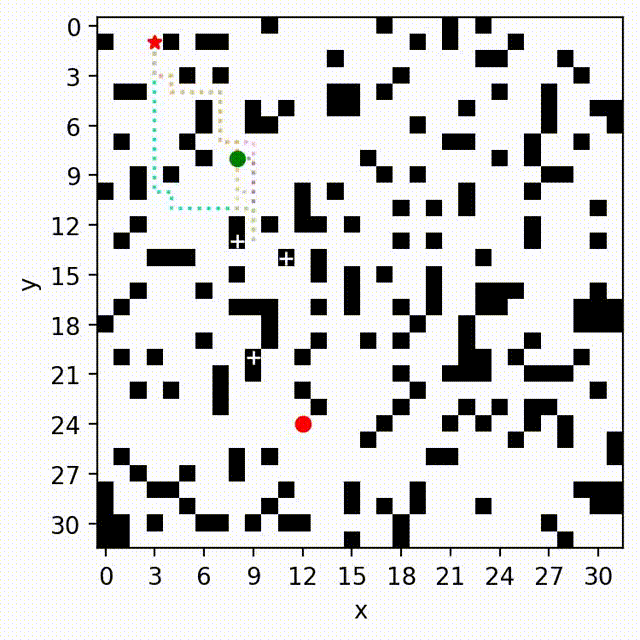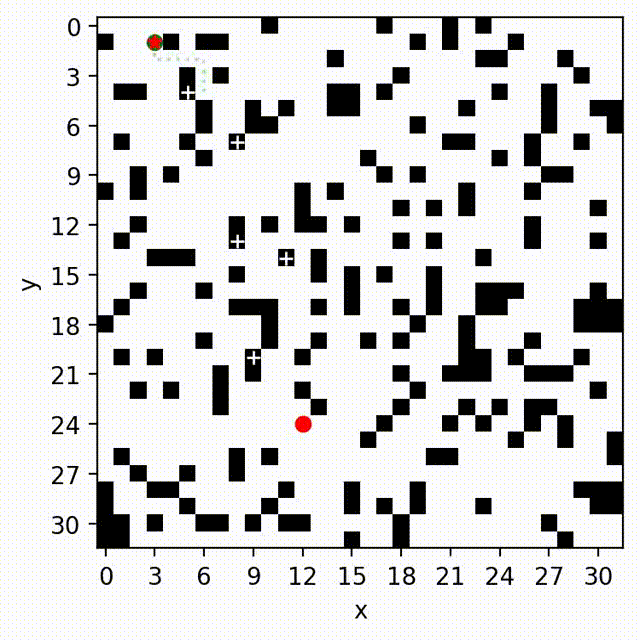
We develop a new multi-objective incremental search algorithm called Multi-Objective Path-Based D* Lite (MOPBD*) which leverages a path-based expansion strategy to prune dominated solutions. Additionally, we introduce a sub-optimal variant of MOPBD* to improve search efficiency while approximating the Pareto-optimal front. We numerically evaluate the performance of MOPBD* and its variants in various maps with two and three objectives. Results show that our approach is more efficient than search from scratch, and runs up to an order of magnitude faster than the existing incremental method for multi-objective path planning. More details can be found in [3].
MO-SIPP: MOPP among Dynamic Obstacles
Path planning among dynamic obstacles is a fundamental problem in Robotics with numerous applications. We investigate a problem called Multi-Objective Path Planning with Dynamic Obstacles (MOPPwDO), which requires finding collision-free Pareto-optimal paths amid obstacles moving along known trajectories while simultaneously optimizing multiple conflicting objectives, such as arrival time, communication robustness and obstacle clearance. Most of the existing multi-objective A*-like planners consider no dynamic obstacles, and naively applying them to address MOPPwDO can lead to large computation times. On the other hand, efficient algorithms such as Safe-Interval Path Planing (SIPP) can handle dynamic obstacles but for a single objective. We therefore develop an algorithm called MO-SIPP by leveraging both the notion of safe intervals from SIPP to efficiently represent the search space in the presence of dynamic obstacles, and search techniques from multi-objective A* algorithms. We show that MO-SIPP is guaranteed to find the entire Pareto-optimal front, and verify MO-SIPP with extensive numerical tests with two and three objectives. The results show that the MO-SIPP runs up to an order of magnitude faster than the conventional alternates. More details can be found in [4].