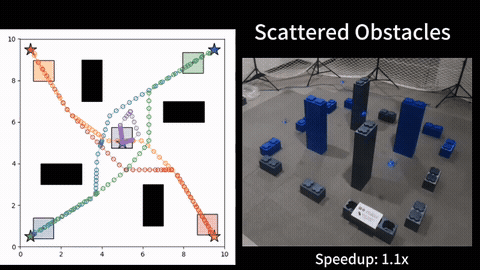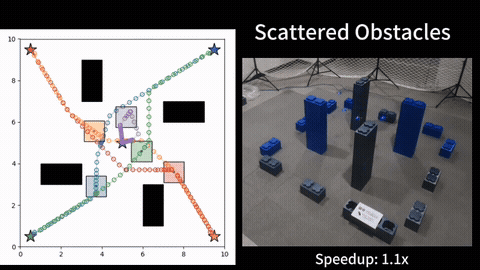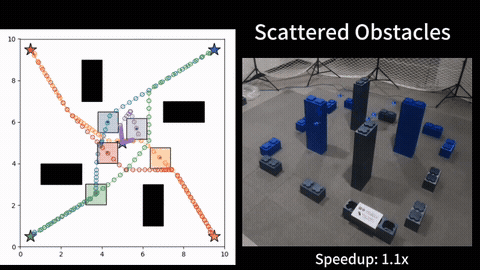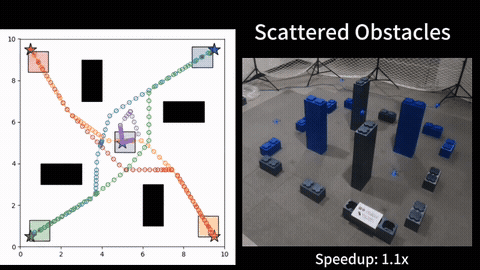
Resource constrained path planning seeks an optimal path subject a variety of resource constraints. This problem arises in applications such as fuel limits or battery capacity in electrical vehicles or package delivery quadroters. These problems are usually NP-hard, and we seek to develop fast planning algorithms to solve these problems to optimality.
Resource Constrained Shortest Path Problem (RCSPP)
We first consider the Resource Constrained Shortest Path Problem (RCSPP), which requires a minimum-cost path between a start and a goal location while ensuring that one or multiple types of resource consumed along the path do not exceed their limits. This problem is often solved on a graph where a path is incrementally built from the start towards the goal during the search. RCSPP is computationally challenging as comparing these partial solution paths is based on multiple criteria (i.e., the accumulated cost and resource along the path), and in general, there does not exist a single path that optimizes all criteria simultaneously. Consequently, the search needs to maintain and explore a large number of partial paths in order to find an optimal solution. While a variety of algorithms have been developed to solve RCSPP, they either have little consideration about efficiently comparing and maintaining the partial paths, which reduces their overall runtime efficiency, or are restricted to handle only one resource constraint as opposed to multiple resource constraints. We develop a planner called Enhanced Resource Constrained A* (ERCA*), a fast A*-based algorithm that can find an optimal solution while satisfying multiple resource constraints. ERCA* leverages our prior research in multi-objective path planning to efficiently compare and maintain partial paths, and techniques from the existing RCSPP literature. Furthermore, ERCA* has a functional parameter to broker a trade-off between solution quality and runtime efficiency. The results show ERCA* often runs several orders of magnitude faster than an existing leading algorithm for RCSPP. More details can be found in [1].
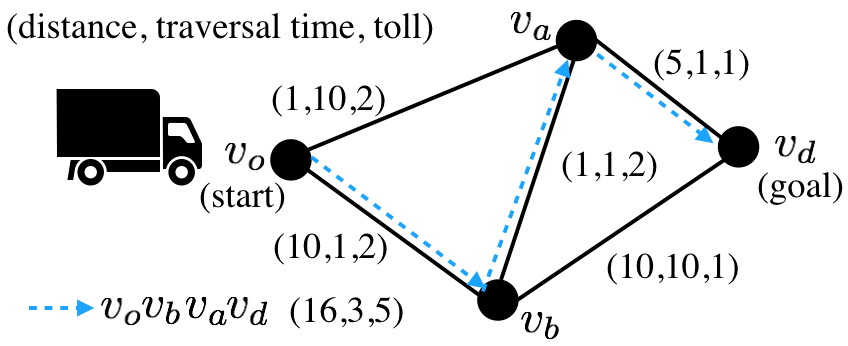
Path Planning with Refueling
We then further consider a specific type of constraint, the fuel constraint of the robot. In this Refueling Path Planning (RFPP) problem, the vertices represent gas stations with known fuel prices, and the edge costs indicate the gas consumption when moving between vertices. The fuel prices at vertices may be different and are fixed over time. RFPP seeks a start-goal path subject to a limited gas tank and a limited number of refuelling stops while minimizing the fuel cost along the path. RFPP is also called the Gas Station Problem in the literature. It arises in applications such as path planning for electric vehicles between cities and package delivery using an unmanned vehicle, where a robot needs to move over long distance when refuelling becomes necessary. While RFPP is polynomial time solvable, it remains a challenge to quickly compute an optimal solution in practice since the robot needs to simultaneously determine the path, where to make the stops, and the amount of refuelling at each stop.
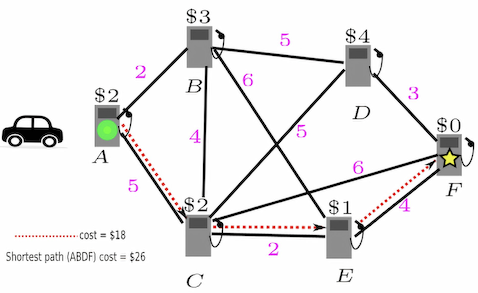
We focus on developing exact algorithms that can solve RFPP to optimality. Based on our research on ERCA*, we develop a heuristic search algorithm called RF-A*, which iteratively constructs partial solution paths from the start vertex to the goal guided by a heuristic function. We compare RF-A* against baselines in real-world city maps of various sizes from the OpenStreetMap dataset. Our results show that RF-A* runs more than an order of magnitude faster than the baseline as tested in maps with hundreds of gas stations. While the baseline takes up to hundreds of seconds to solve these test instances, RF-A* often takes less than a second. The fast running speed makes it possible for online planning on a robot with a limited tank in large urban areas. More details can be found in (missing reference).